终于来到Andrew Ng教授深度学习专项课程CNN课程的的最后一节课的笔记博客了，这也是这门课程专栏的最后一篇博文了，本篇主要内容主要是CNN在人脸识别和神经风格迁移中的应用。那我们开始吧！

人脸识别

人脸识别简介

什么是人脸识别？我想大家应该都使用过人脸识别的系统，比如一些办公楼或者小区的人脸识别系统，系统可以识别到一个活生生的人脸（相比于照片或者ID卡上的图像）。它的应用可以让人们更方便地进入一个地方，而不需要携带ID卡。这个系统结合了人脸识别和活体检测。

在人脸识别领域，我们通常讨论的是人脸验证和人脸识别这两个问题。

• 人脸验证问题（一对一问题）: 给定一张输入图像和一个人的名字或ID，系统需要验证输入图像是否是该人。
• 人脸识别问题（一对多问题）: 更难，需要从一个数据库中识别出输入图像的人脸。比如，一个数据库里有100个人，系统需要从这100个人中找出输入图像的人脸。这种情况下，即使你的人脸验证系统有99%的准确率，对于人脸识别系统来说，错误的可能性也有100倍的增长。因此，如果你希望人脸识别系统的错误率在可接受范围内，你可能需要一个准确率远超过99%的人脸验证系统。

One Shot Learning（单次学习问题）

面部识别应用跟其他常见的神经网络使用场景不同，它通常需要能够通过一个单一的图像或该人脸的一个例子识别一个人。事实上，如果只有一个训练样例，深度学习算法的效果并不好。

一个可能的解决方法是学习一个相似性函数。具体来说，你想让神经网络学习一个函数（记为d），该函数输入两个图像并输出两个图像之间的差异程度。如果两个图像是同一个人，你希望函数输出一个小的数字；如果两个图像是两个完全不同的人，你希望它输出一个大的数字。

在验证时，如果两张图片的差异程度小于某个阈值\tau （超参数），则可以预测这两张图片是同一个人。如果大于这个阈值，则预测这是不同的人。要将其用于识别任务，你会使用函数d比较新的图片和数据库中的图片。你将对数据库中的其他图像执行此操作，然后基于此，你可以找出这实际上是哪个人。

因此，如果你的团队中有新人加入，你可以将第五个人添加到数据库中，这样就可以正常工作了。

孪生网络（Siamese network）

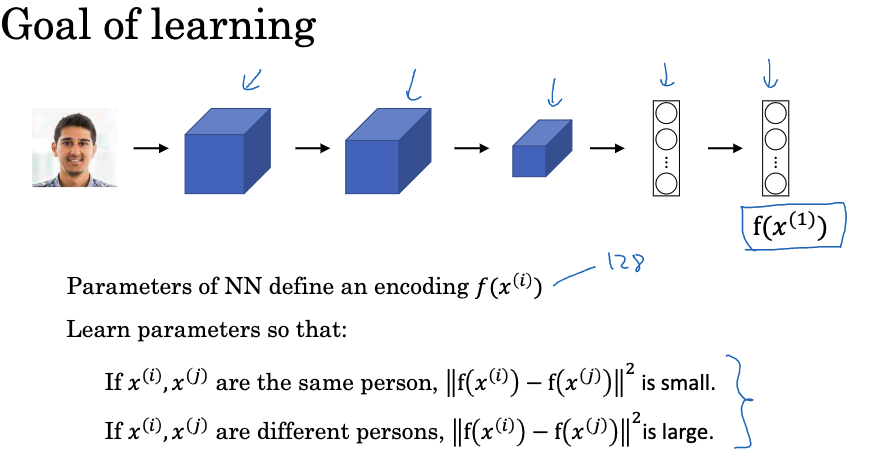
孪生网络是一种可以帮助我们处理单词学习问题的一种技术，一个孪生网络包含两个完全相同的神经网络，它们共享参数并一起训练。每个网络接收一个输入并输出一个向量，这个向量可以被看作是输入图像的编码。孪生网络通常用于比较两个不同的输入，例如在人脸识别任务中，它就是比较两张面孔。

它里面的编码是指经过神经网络处理后的一组特征向量，包含了输入图像的关键信息。例如，对于人脸识别任务，神经网络将接收一张脸的图像作为输入，然后输出一组数字，这组数字就是这张脸的编码。

神经网络的目标是学习一个函数d，该函数输入两张脸的图像，并输出这两张脸的编码之间的差值的范数。如果这两张脸属于同一个人，那么这个差值应该很小；如果这两张脸属于不同的人，那么这个差值应该很大。这可以通过反向传播和梯度下降等优化算法来实现。

Triplet Loss

接下来我们再看一个叫做三元组损失函数的概念，三元组损失函数（Triplet Loss Function）的应用需要比较一组图片。在这组图片中，有一个锚定图片（Anchor）, 一个正样本图片（Positive）和一个负样本图片（Negative）。正样本是与锚定图片同一人的图片，而负样本是不同人的图片。

我们肯定是希望锚定图片和正样本图片的编码相似，因为他们是同一个人。而锚定图片和负样本图片的编码希望是非常不同，因为他们是不同的人。

因此锚定图片与正样本图片的编码距离应对小于锚定图片与负样本图片的编码距离。此外，为了防止神经网络给出简单输出（比如输出全为零或者所有图片的编码都相同），还引入了一个边缘参数（Margin），它使得正负样本之间的距离需要大于这个边缘参数。这个边缘参数是另一个需要调整的超参数。

为了使训练更加有效，应选择那些“难”训练的三元组进行训练。这样可以增加学习算法的计算效率，因为随机选择的三元组往往太容易满足约束条件，神经网络从中学不到什么。对于“难”的三元组，学习算法需要尝试更加努力才能满足约束条件。

为了训练神经网络，你需要有许多包含三元组的训练集，然后使用梯度下降法尝试最小化定义的损失函数。这样，反向传播将会影响神经网络中所有的参数，使得神经网络学习到一个好的编码，使得相同人的图片的距离小，不同人的图片的距离大。

在进行人脸识别训练时，通常会使用大量的数据集。这些数据集通常包含超过百万或千万级别的图片，因此，下载他人预先训练好的模型可能比从头开始训练更为实用。

Face Verification and Binary Classification

接下来再介绍一种将人脸验证问题作为二分类问题来解决，这是一个对三元组损失函数的替代方案。

这种方法的训练方式是，通过一个双生神经网络（Siamese Network），计算两个面部图像的嵌入（也可以是更高维度的嵌入），然后输入到一个逻辑回归单元中进行预测。目标输出是1，如果这两个图像是同一个人；目标输出是0，如果这两个图像是不同的人。

逻辑回归单元的输出ŷ 是应用于一组特征的sigmoid函数。这里，我们不是直接输入这些嵌入，而是计算嵌入之间的差异。

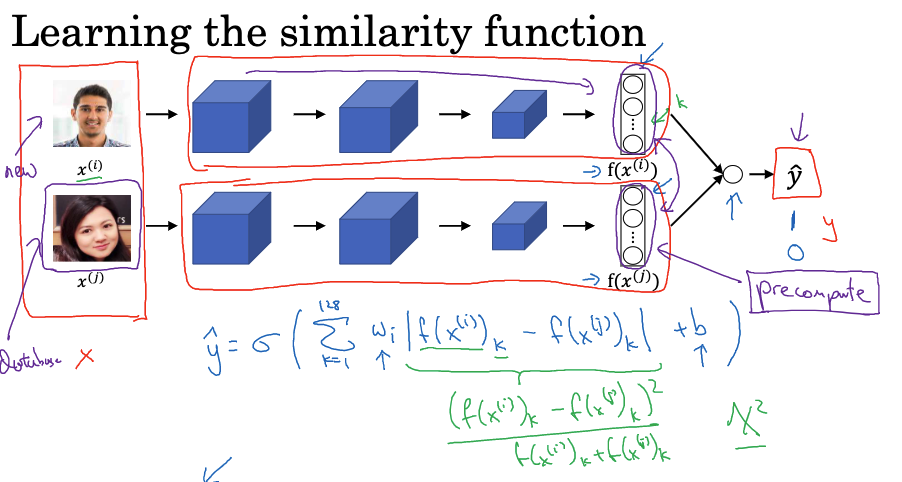
假设将绝对值差异（元素对元素）作为特征输入到逻辑回归中。对于这128个数字，可以认为它们是需要喂入逻辑回归的特征。然后，可以训练适当的权重以预测这两个图像是否属于同一人或不同的人。在计算公式时有其他的变体，例如卡方相似度公式。这种变体在深度脸部（DeepFace）论文中也有探讨。在这种学习公式中，输入是一对图像，输出y是0或1，取决于输入的是相似图像对还是不相似图像对。

双生神经网络在训练中共享参数，这意味着上面的神经网络的参数与下面的神经网络的参数绑定在一起。当有新的图像出现时（例如新的员工），可以预先计算嵌入，然后当新员工出现时，使用神经网络的上部分计算新的嵌入，并将其与预先计算的嵌入进行比较，以进行预测。这种预计算技巧可以显著节省计算时间。为了将人脸验证视为监督学习，可以创建一组图像对作为训练集，其中目标标签是1，当这些图像对属于同一人时；目标标签是0，当这些图像对属于不同的人时。然后使用这些对来训练神经网络。

综上所述，将人脸验证和人脸识别视为二分类问题是一种非常有效的方法，可以进行一次学习。

神经风格迁移

神经风格转移（Neural Style Transfer）是卷积神经网络（ConvNet）的最有趣和令人兴奋的应用之一。神经风格转移允许你将一种艺术风格应用于另一张图像，从而生成一种新的艺术作品。

例如，可以使用梵高的“星夜”画风重塑一张斯坦福大学的照片，或者使用毕加索的画风重塑一张金门大桥的照片。在神经风格转移中，用"C"表示内容图像，用"S"表示风格图像，用"G"表示生成的图像。要实现神经风格转移，需要查看ConvNet在各个层级，从浅层到深层，提取的特征。

深度卷积网络到底在学习个啥？

想知道网络中每一层内部的秘密，可以通过寻找最大化特定单元激活的图像或图像块，可视化各个层级的隐藏单元正在计算什么。

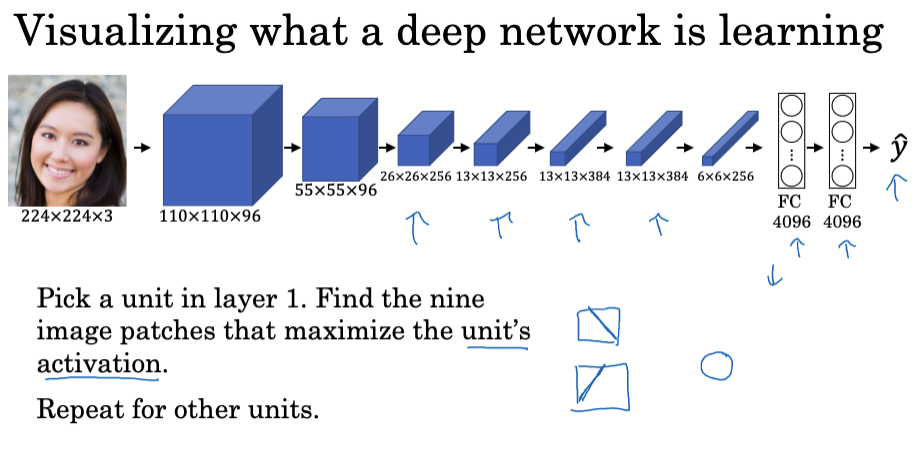
例如，在第一层的隐藏单元可能会查找相对简单的特征，如边缘或特定颜色的阴影。进入更深的层次，隐藏单元开始检测到更复杂的形状和模式。

在第二层，某些隐藏单元可能对含有许多垂直线条的纹理或左侧具有圆形形状的图像产生高度激活。

在第三层，隐藏单元开始检测更复杂的模式。例如，某些单元可能对左下角有圆形形状的图像反应强烈，甚至开始检测出车辆、狗，甚至是人。另一些单元可能会对某种特定的纹理（如蜂窝状或方块状）反应强烈。

在更深的层次（如第四层和第五层），隐藏单元开始检测出更复杂的对象。例如，某些隐藏单元可能已经学会了检测水，或鸟的腿，或者甚至是特定种类的狗。第五层的单元甚至能够检测出更为复杂的物体，如键盘或者花。

从这些观察中，我们可以得出一个结论：在卷积神经网络中，较浅的层次往往学习更简单的特征（如边缘和颜色），而较深的层次则能学习更复杂的特征，甚至是对象。

这种对神经网络层次计算内容的理解，为下一步构建神经风格转移算法奠定了基础。

成本函数 （Cost Function）

如何使用成本函数建立神经风格转移（Neural Style Transfer）系统，并通过最小化成本函数生成想要的图像呢？

首先，假设我们有一个内容图像C，一个风格图像S，我们的目标是生成一个新的图像G。为了实施神经风格转移，我们将定义一个 Cost function: J(G)，该函数衡量特定生成图像的好坏。我们将使用梯度下降来最小化J(G)以生成这个图像。

“好坏”如何定义？我们将在这个成本函数中定义两部分。第一部分叫做"内容成本"，它是内容图像和生成图像的函数，衡量的是生成图像的内容与内容图像C的内容有多相似。第二部分是"风格成本"，它是风格图像S和生成图像G的函数，衡量的是生成图像G的风格与风格图像S的风格有多相似。

最后，我们将使用两个超参数alpha和beta来指定内容成本和风格成本之间的相对权重。

要运行这个算法，你需要初始化生成的图像G（随机初始化），然后定义前面幻灯片中的成本函数J(G)。然后，你可以使用梯度下降来最小化J(G)，通过更新图像G的像素值。

例如，如果你从这个内容图像和这个风格图像开始，当你随机初始化G时，你最初随机生成的图像就是这个白噪声图像，每个像素值都是随机选择的。当你运行梯度下降，通过慢慢调整像素值来最小化成本函数J(G)，你会慢慢得到一个越来越像你的内容图像，但是以你的风格图像的风格呈现出来的图像。

内容成本函数

在神经风格迁移算法的成本函数中，内容成本函数是一个重要的组成部分。内容成本函数主要用于测量生成的图像与内容图像之间的内容相似度。

决定内容成本的计算是在网络的哪一层进行。如果选择浅层，将会强制生成的图像的像素值非常接近内容图像。如果选择深层，只要生成图像中有内容图像的元素即可（如：内容图像有一只狗，生成的图像中也需要有一只狗，但位置可变）。通常，我们选择中间层进行计算，以平衡这两种情况。

使用预训练的ConvNet（如VGG网络）计算内容图像和生成图像在选定层的激活。如果这两个激活相似，那么两个图像的内容可能也相似。

定义内容成本函数J_content(C,G)为两个激活之间的元素差的平方。此处，可以添加一个规范化常数。这个常数可以通过超参数alpha进行调整。注意，这个计算过程中，激活被展开为向量。

在后续的梯度下降过程中，这个内容成本函数将鼓励算法找到一个图像G，使得其在特定隐藏层的激活与内容图像的激活相似。

风格成本函数

图像的风格可以定义为在某个特定层的激活之间的相关性。这种相关性测量了图像中不同特征之间的相关性。

给定一张图片，我们可以计算出一个风格矩阵G，用以测量上述相关性。具体公式如下图所示。

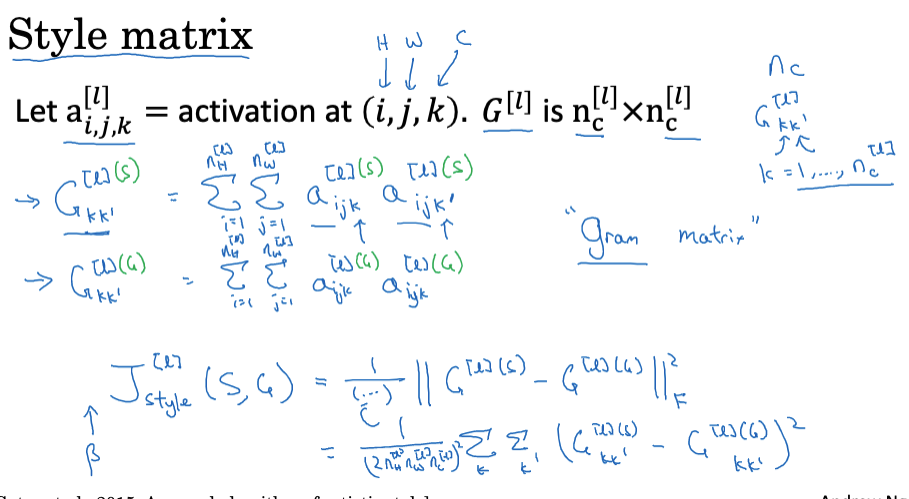
一旦我们有了风格矩阵，就可以定义风格成本函数。这个成本函数计算了生成的图像与风格参考图像的风格矩阵之间的差异。具体来说，这是两个风格矩阵元素的平方差的和，即Frobenius范数的平方。

在实践中，我们通常使用来自多个不同层次的风格成本函数，从而考虑图像的低级特征（如边缘）和高级特征。这些风格成本函数被一个特定的权重系数λ进行加权后求和，得到总体的风格成本函数。

我们的目标是找到一个图像G，使得内容成本函数与风格成本函数的加权和最小。形式化地表示，总体成本函数J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G) ，然后尝试最小化这个成本函数。

这就是神经风格迁移的核心思想。使用这个方法，我们可以生成具有新颖艺术风格的图像。

### 1D and 3D Generalizations

我们已经学习了很多关于卷积神经网络的内容，包括网络的结构、如何用它进行图像识别、对象检测、面部识别和神经风格转换。尽管我们主要关注2D图像数据，但这些理论也同样适用于1D和3D数据。

前面的博客中，我们学习了2D卷积，比如你可能将一个14×14的图像和一个5×5的过滤器进行卷积，结果得到一个10×10的输出。如果有多个通道，比如14x14x3的输入与5x5x3的过滤器进行卷积，如果有16个过滤器，最后的输出会是10x10x16。

类似的思想也可以应用于1D数据。比如左边的一个心电图(EKG)信号，它是一个时间序列，显示了每个时间点的电压。你可能只有一个14维的输入，然后用一个1维的过滤器去卷积，得到的输出就是10维的。如果有多个通道，可能有16个过滤器，那么结果就是10×16的。

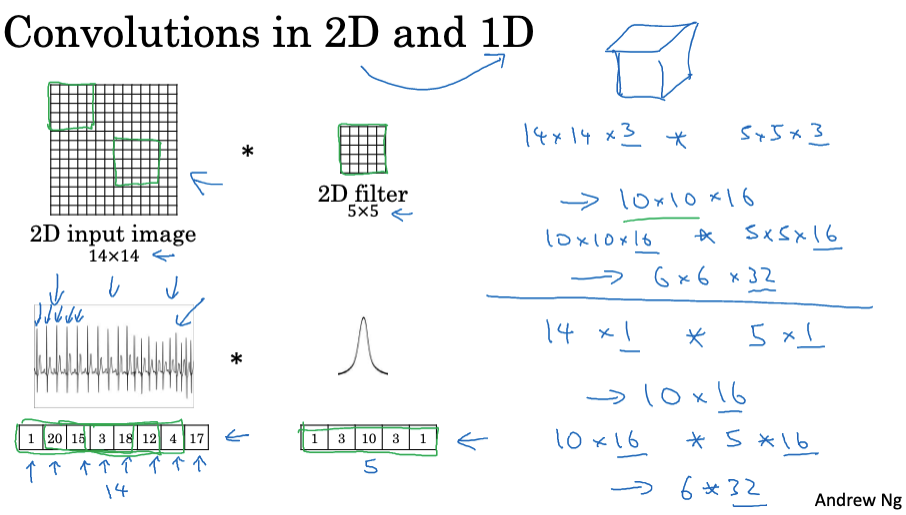
卷积神经网络的另一层可能会将10×16的输入与5维的过滤器进行卷积，得到6×32的输出。所有这些思想也适用于1D数据，它可以在多个位置检测同样的特征。

那么对于3D数据呢？3D数据，就是你现在有一个3D块，一个三维的输入体积。比如CT扫描给出了你身体的三维模型，你可能会有14x14x14的输入，进行5x5x5的过滤器卷积，得到10x10x10的体积。

卷积神经网络(ConvNets)虽然大部分用在处理2D数据，但其理论和模型也可用于处理1D数据和3D数据，使得ConvNets更具灵活性和应用范围。

总结

以上就是关于人脸识别以及神经风格迁移的知识点内容，也是深度学习专项课程的最后一节课程的博客啦。真的非常感谢各位的观看。完结撒花！🌺 🌺 🌺 🌺 🎆 🎆 🎆

附录-相关文献

1. Taigman Y, Yang M, Ranzato M A, et al. Deepface: Closing the gap to human-level performance in face verification[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2014: 1701-1708.
2. Schroff F, Kalenichenko D, Philbin J. Facenet: A unified embedding for face recognition and clustering[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 815-823.
3. Matthew Zeiler D, Rob F. Visualizing and understanding convolutional neural networks[C]. ECCV, 2014.
4. Gatys L A, Ecker A S, Bethge M. A neural algorithm of artistic style[J]. arXiv preprint arXiv:1508.06576, 2015.